Learning cp again, i suppose

https://www.codechef.com/problems/PRODEQSUM

Premise of the problem: given an array $A$ of length $N$, find the number of good subarrays, count all the pairs, ($L, R$) which satisfy its $\prod = \sum$

Observation 1

• Let’s assume no elements in the subarray is equal to $1$, and the current product is $P$, the current sum is $S$. Assume $S = P$
  • Adding another element $X$
  • $XP > P + X$
  • $(X - 1)P > X$

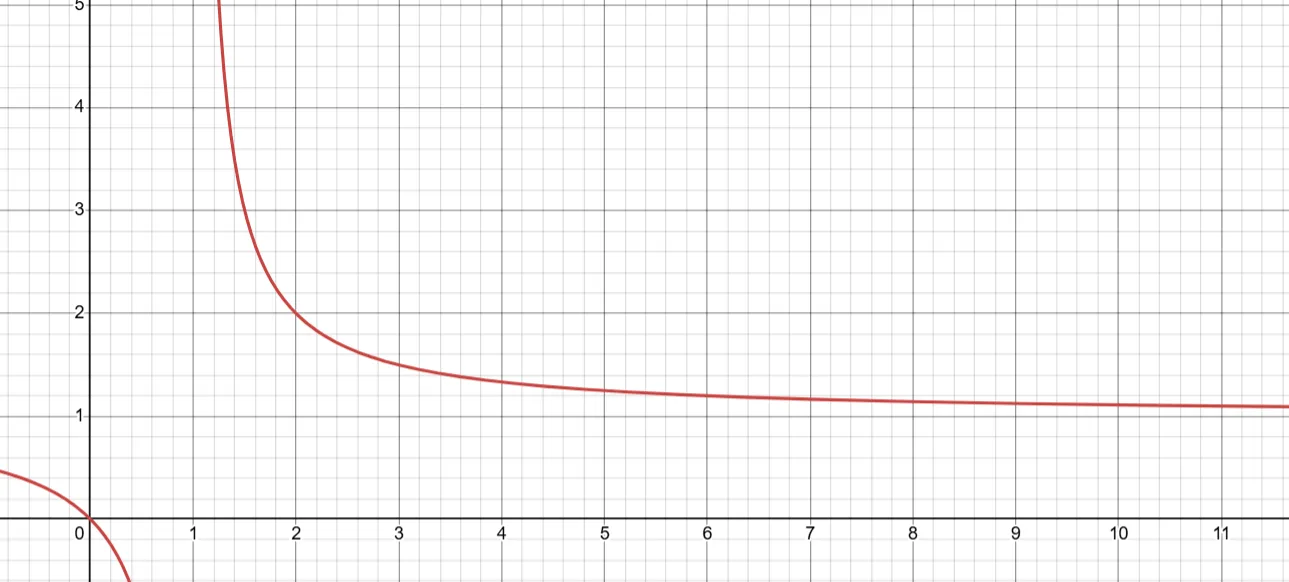
• Assume it’s 1
  • It will increase the sum counterpart while the product counterpart stays the same value.
  • This is good for increasing sum.

Observation 2

Let’s count some lower bounds

Imagine if there are 5 elements, all 2.

Lets make the notation $F(x, y) = (S, P)$ for having $x$ elements of $y$

• $F(5, 2) = (10, 32)$, different is $22$
• $F(10, 2) = (20, 1024)$
• $F(17, 2) = (34, 131072)$

So we observe that maximum non-1 elements are only 17, no more, because it’s not possible for us to construct a subarray that has $18$ of $2$s, and less than $200\,000 - 18$ amount of $1$s

We can run a $17N$ algorithm,

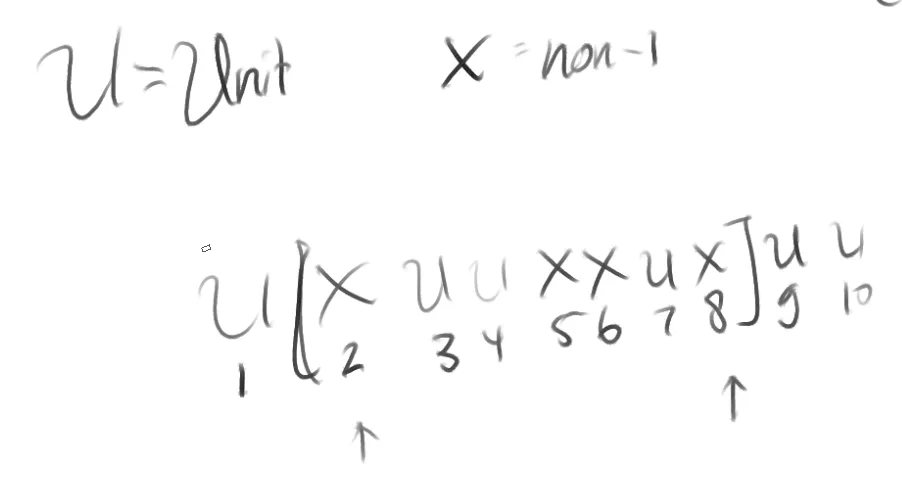
I’m proposing this solution to count each of this candidate pairs, which candidate ends are non unit, and we count the $S - P$ difference for that candidate subarray, and then count how many units are needed to be added to make the array good. Count how many are available in the left and right of the subarray, and then apply a linear arithmetic count.